Valispace has a sister site whatsthatformula.com, that lists lots of common formulas that engineers use when building complex hardware.
So next time you’re scratching your head struggling to remember the exact formula for the gravity gradient, just think WTF!? What’s That Formula!
From time to time, we like to explore the context of some of the formulas that have changed our world. Today, we explore Bernoulli’s law.
The Bernoulli Equation
Bernoulli’s principle describes a fluid’s behaviour under varying flow and height conditions. It states that an increase in the speed of a fluid occurs simultaneously with a decrease in static pressure or a decrease in the fluid’s potential energy. The equation is formed by the following variables:
P – Static pressure
p – Fluid Density (in kg per cubic meters)
v – Fluid Flow velocity (in meters per second)
h – Height above reference surface
g – acceleration due to gravity
The history of the Bernoulli principle
The principle is named after Swiss mathematician and physicist Daniel Bernoulli, who published it in his book Hydrodynamica in 1738.
He conducted experiments in energy conservation using fluids, observing how water flows through pipes of varying diameters. In a segment of a pipe with relatively large diameter he observed that water flowed slowly, but as it entered a smaller diameter segment, its speed increased.
Although Bernoulli deduced that pressure decreases when the flow speed increases, Leonard Euler derived Bernoulli’s equation to its usual form in 1752.
Real-world applications of the Bernoulli principle
The principle states that as the speed of a fluid increases, its pressure decreases, and vice versa. This relationship can be observed in various situations, such as the flow of air over an airplane wing, the flow of water through a pipe, and the flow of blood in a human artery.
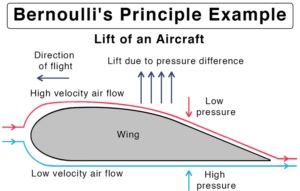
One of the most well-known examples of Bernoulli’s principle is the demonstration in which a stream of air is directed over the top of a curved surface, such as an airplane wing.
The air moving over the curved surface is forced to travel a greater distance than the air moving underneath the wing, and as a result, it must move faster in order to cover that distance in the same amount of time.
As the speed of the air increases, its pressure decreases, which creates a lifting force that helps to keep the airplane in the air.
Another example of Bernoulli’s principle can be seen in the flow of water through a pipe. As the water flows through the pipe, it is forced to move faster in the narrow sections and slower in the wider sections.
This change in speed causes a corresponding change in pressure, with the water experiencing a higher pressure in the wider sections and a lower pressure in the narrower sections.
The Bernoulli principle also applies to blood flow in the human body. Blood vessels have varying diameters, and as the blood flows through them, it moves faster in the narrower vessels and slower in the wider vessels.
This change in speed causes a corresponding change in pressure, with the blood experiencing a higher pressure in the wider vessels and a lower pressure in the narrower vessels. This pressure difference helps to pump blood throughout the body.
Bernoulli’s principle also has some practical applications, such as in fluid flow meters, which measure the speed of a fluid and use that information to determine the fluid’s volume or flow rate.
Another application is the Venturi tube, which is used to measure the flow rate of fluid in a pipe. A Venturi tube is a constriction in a pipe that causes the fluid to move faster and experience a decrease in pressure as it flows through the constriction.
This decrease in pressure can be measured and used to calculate the fluid’s flow rate.
In conclusion, Bernoulli’s principle is a fundamental concept in fluid dynamics that explains how the speed of a fluid affects its pressure.
It can be observed in various situations, such as the flow of air over an airplane wing, the flow of water through a pipe, and the flow of blood in a human artery. It has various practical applications, such as in fluid flow meters, Venturi tubes and many more.